ClassJack: developing an intuition for probability logic

Off the Desk. Probability Logic Volume 2

This post explores a game developed with my colleague (Kelly Legacy), and TAs (Greg and Matt). Greg had the initial idea to play blackjack to help students develop an intuition for probability logic. Students have a chance to experience the advantages that are associated with counting cards in an environment that makes it easier to do so. The background of my history with probability logic was set forth in Volume 1 (here).

Blackjack

Blackjack is a card game with the goal of getting as close to 21 points as possible, without going over 21 points. Cards 2-9 have the respective point value 2-9; cards 10, Jack, Queen, King have the point value 10; and Ace can either be 1 or 11 points. A deck of cards has 52 cards, 4 each for each point value between 2 and 9 (32 cards), 16 cards worth exactly 10 points, and 4 Aces. With a complete and well shuffled deck the probability of being dealt a card worth 10 points is about 31%. The dealer distributes two cards - both face up - to the players; and two cards to themself. One of the dealer cards is face down (unknown information). Players take turns deciding whether to “hold” or “hit”. Hit means being dealt another card. If on the initial deal a player has a 2 and an 8 (total of 10 points), they would easily choose to “hit” because they cannot go over 21 (nothing to lose), and will certainly get closer to 21. How much closer to 21 they get depends on the card dealt, which depends on the cards in the deck.

Blackjack to learn about probability logic

The first iteration to playing blackjack in the classroom to learn about probability logic started by making it easier to count cards by providing a card counting cheat sheet. As a side note, it is not illegal to count cards. Casinos don’t allow it, even in your head, which is quite bizarre if you think about it. It’s like telling a chess player they can only play if they don’t think about what the best move is in the game. A casino would certainly not allow a player to sit with a notebook and a card counting cheat sheet and a calculator. To test out this scenario we played blackjack with 2 decks of cards. Casinos, I am told, use several decks of cards and I’m not sure if they let you know how many decks are being used. We played as a team that could communicate. Kelly was making decisions, Matt was counting cards with the cheat sheet, and I was calculating probabilities. We had as much time as we needed to count, make calculations of different probabilities, and then make decisions. Greg was the dealer - and he has actual casino blackjack playing experience. Greg played as a casino dealer would play; with 17 being a necessary “hold” or “hit” threshold (anything under 17 he must hit; at or above 17 he must hold).

Counting the cards played meant that as we played the game we learned which cards were remaining in the deck. This was our model of learning. We were learning was the probability of an event that would follow from an action (“hit” being the action). The event could be “getting an Ace” or it could be “getting a number > 8” or “getting a number < 6” - defining the event was just as much part of the strategy as was calculating the probability of that even occurring.

To frame a decision to “hit” as a deduction using probability logic in the case of having two cards that sum to 13 points (where you’d want a card <=8, and not want a card > 8):

Premise 1: I want a card <=8

Premise 2: There are 16 out of 24 cards left that are <= 8 (P(<=8|this deck) = 66%)

Premise 3: Hit - action decision based on P(<=8|this deck) = 66% (odds of being dealt a card <= 8 = 1.9:1)

Conclusion: Card <= 8 (true 66% of the time; odds of this being true 1.9:1)

The decision is nuanced and more challenging as the P(<=8|this deck) approaches 50%. The further from 50% the easier the decision - either towards 100% (definite hit), or towards 0% (definite don’t hit).

The decision is nuanced based on the dealer’s hand for two reasons. Remember, the dealer’s hand is partially unknown. Since the team must get closer to 21 than the dealer they are influenced by the one card showing in the dealer’s hand. If the dealer is showing a 10 card, the team is more likely to take a risk. A risk would be a hit with a less than 50% probability of being dealt a card you need. Another nuance based on the dealer’s hand is the unknown information of the face down card. The probability calculated for pulling a card is now an estimate because we don’t know one of the cards. It is more realistic - we don’t usually know precise probabilities - but for a class game to demonstrate an intuition to using probabilities and experiencing learning through understanding probabilities I wanted to eliminate this nuance in the game. These two nuances are the major reason that for an introduction to developing an intuition of probability logic we created ClassJack. The added nuance of blackjack is something that we need more time to consider. Blackjack adds a deeper level of decision making to the game for future class activities.

The metric for assessing whether the team was getting better as we moved through the game was whether we won a hand or not. The goal, and hypothesis, was that we would win more of the hands in the second half of the game than the first half. For example, if it took 16 hands to get through the 2 decks of cards, then what proportion did we win in the first 8 hands vs. the second 8 hands?

This first trial (of blackjack) was successful overall, with 4/8 (50%) hands one for the first half, and 5/8 (62.5%) hands one in the second half of the game. Not bad considering the nuances of the dealer hand. If played correctly over time in a casino we would leave with more money than we arrived. Another nuance that we did not introduce at all was the issue of actual betting - and I’m sure there are more as Greg kept interjecting the many added complexities of blackjack casino (splitting, doubling down…, etc).

Blackjack to ClassJack

ClassJack attempts to remove the nuance of the dealer from the game to focus on a simplified decision making scenario using probability logic. It’s a model, all models are wrong, some models are useful. The goal is a less complicated model of decision making about actions with information about probabilities. Future versions can incrementally include the dealer until once again becoming blackjack.

Each team in ClassJack is dealt a hand from their own deck of cards. Just one deck. The dealer is not dealt a hand. As cards are played the players see them and can immediately recalculate the probability of future events. Events are defined as needed depending on the situation. The players can keep all cards played face up on a table arranged as they see fit - ideally in a way that facilitates the calculation (or even just observation) of the probabilities. For example, if you see that all of the cards that equal 10 are on the table, you know that the probability of being dealt a card equal to 10 is 0. This simple adjustment (not allowed at a casino) makes card counting MUCH EASIER. The goal of the game is to get as close to 21 as possible, ideally without going over 21 (which carries a stiffer penalty to your score).

The scoring algorithm we’ve settled on for now - but which could be revised any number of ways - is based on a sum of squared differences.

The squared difference for a hand is the square of the difference between 21 and the points of the hand (21 - points)^2. Each hand the squared differences are summed. To add a penalty to going over 21, the calculation of a hands squared difference includes a “2x” multiplier prior to squaring. If your hand has 26 points: ((21-26)*2)^2 = 100; as opposed to 16 points: (21-16)^2 = 25. In both cases the team is 5 points away from 21, but going over results in 4x the points.

The goal of ClassJack is to have the lowest point total. The teams (of 2-3 students) are playing with their own deck of cards, but they are playing against each other. A “perfect game” would have a score of 0. Always achieving a score of 18 would result in a total score - after 16 hands - of 144 points. Both highly improbable scenarios. It may be impossible actually. I have not taken the time to figure out mathematically whether there is a perfect way to combine the 52 cards of a deck into 16 sets that equate to 18; or whether it is possible to combine 52 cards of a deck into X sets that all equate to 21.

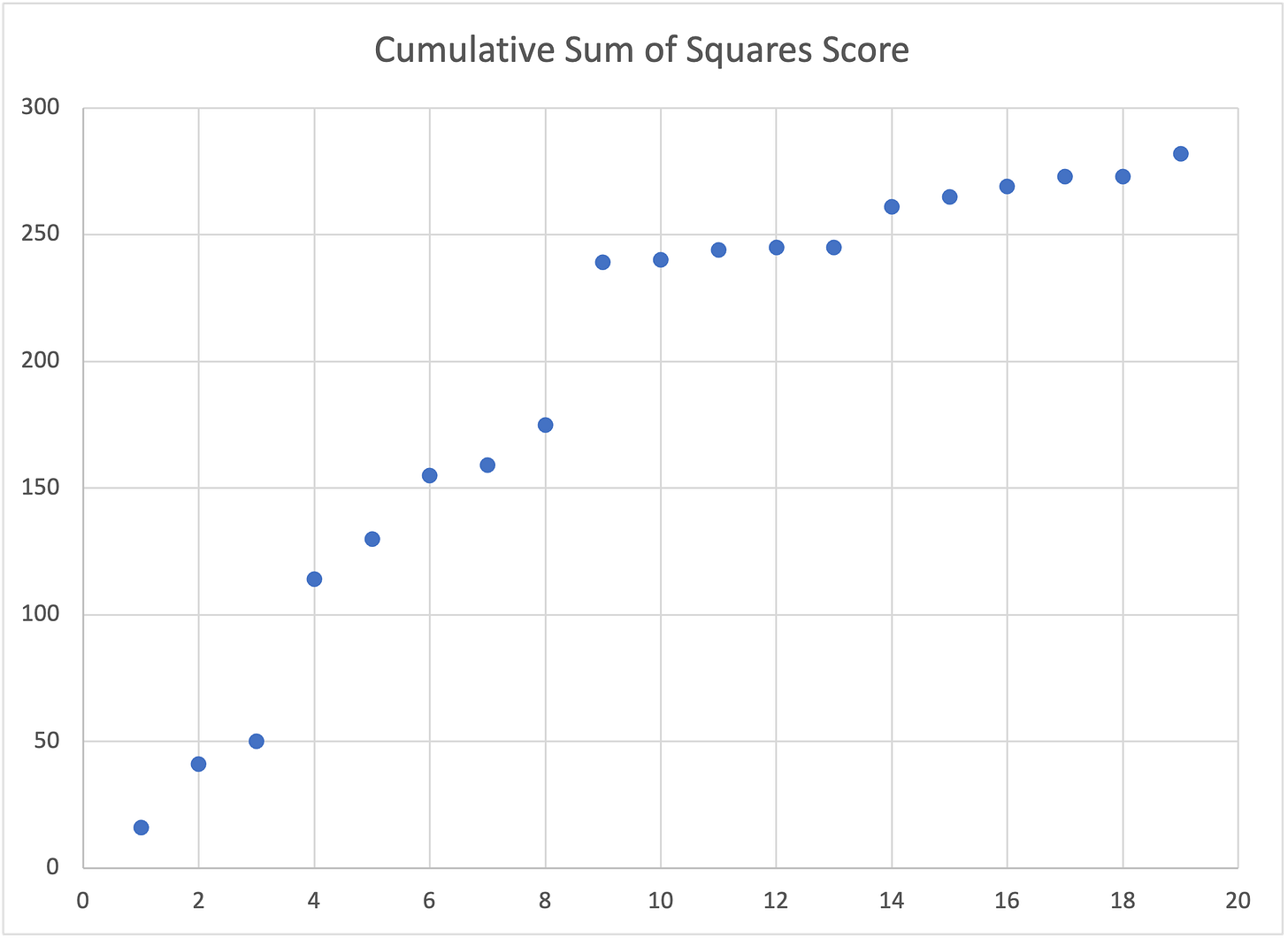
A plot of the hand played (x-axis) and the cumulative sum of squared differences (y-axis) provides a graphic history of the game. If the cumulative sum progress is well described by a line then the game progressed linearly and the team did not seem to take advantage of what they were learning about the probability of events. If the cumulative sum progress plateaus then the team did seem to capitalize by learning about the probability of events.

End game scenarios are difficult and may lead to large score deviations if not handled appropriately. In our pre-class experiments we did not have much experience (played 3 games). But we were able to derive a preliminary rule. If the deck has <3 cards left at the end of a hand, the game is over. Otherwise, they must play another hand. There is no situation where there is a benefit to playing when there are 2 cards remaining. With any two cards that don’t sum to 21 there’s a need to add points despite the inability to “hit”. But with 3 cards remaining that option remains. If there is only 1 card remaining then the team cannot play. A future deviation of scoring could include dividing the cumulative sum of squares score by the number of hands played. This leaves the option open to play with just two cards remaining if you know that the squared difference for that one hand would be less than your current average points per hand, and truly beneficial if it was 21 (adds 0 to the numerator and 1 to the denominator). But since our current goal for ClassJack was to simplify, we held off on this approach to scoring for now.

We played three games. The games included 19, 18 and 19 hands (mean = 18.66); with scores of 219, 293 and 282 (mean = 264.66). The lowest scoring game (game 1) had a run of luck for 4 hands in the early game depicted by the flat “Cumulative Sum of Squares Score” plot. The x-axis depicts the “hand played” and the y-axis depicts the cumulative sum of squares score. The jump up from one hand to the next represents the score for that hand. For example, in Game 1 (below), hands 4 and 15 had the highest jump in score.

Game 1 - a string of luck at the beginning between hands 4 and 7 (x-axis)

Games 2 and 3 both show the expected characteristic “learning curve” for this game - which includes a plateau as players know more about the deck of cards they are playing with and can make more probabilistically informed decisions:

Game 2 - some luck at the beginning followed by learning around hand 8 (x axis)

Game 3: challenged early game, learning started with hand 10 (x axis)

Our hypothesis is that the learning curves in games 2 and 3 are due to knowing the probabilities and having it influence decision making. This is difficult to separate from simply learning how to play the game better (knowing the probabilities AND using them better in decision making).

In the next two weeks we’ll play the game in two sections of the Clinical Inquiry I course in about 8-10 teams of 2-3 students per team. We hope each team can play about 3 games.

An excel spreadsheet that keeps score is available upon request (either by email or by asking in the comments section). If things go well - maybe we’ll make an app.

Probability Logic Volume 3 (forthcoming) expands on the empirical data about the game playing experience (including the curves identified); and will dig deeper into the lessons learned with further connections to probability logic and clinical decision making. For example, information theory to consider the value of information (information increases as the known probability of an event moves further from 50%).